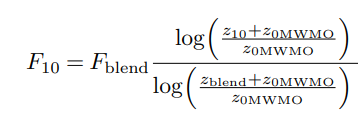Hi all,
I have a short questions regarding the interpretation of wind speed data for the product "ERA5 hourly data on single levels from 1979 to present" [1]. It would be great if you could give me a hint and/or point me to corresponding documentation.
For the "forecast" products, I found the following information: "These '10m wind components' are diagnostic quantities generally computed not by using the roughness length of the tile itself, but instead assuming a roughness length for short grass (=0.03m), the surface over which (by WMO convention) winds should be measured" [2].
My question are:
- Do variables "10m wind component" (u/v) in the product [ 1 ] refer to 0.03 m surface roughness length as described above and thus do not relate to the actual (land cover averaged) roughness of the respective grid cell?
- Do variables "Forecast surface roughness" and "Friction velocity" relate to the actual (land cover averaged) roughness of the respective grid cell?
I assume that the "100 m wind component" (u/v) variables are relatively unaffacted by assumptions about surface roughness because they are far above the "blending height" (40m) as mentioned in [ 2 ].
Thanks in advance for any help on these questions!
Best regards,
Andi
[1] https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-single-levels?tab=overview
[2] https://confluence.ecmwf.int/display/FUG/9.3+Surface+Wind
For the record, I found the answer after some searching in the technical documentation. The ERA5 10m wind speeds do not refer to the grid-cell average wind speed. Instead, they refer to a a roughness length for short grass (=0.03m).
ECMWF. 2021. IFS DOCUMENTATION – Cy41r2. PART IV: PHYSICAL PROCESSES. Reading, UK; 2021. Available at: https://www.ecmwf.int/en/publications/ifs-documentation.
What about wind speed at 100 m? The documentation doesn't mention how that is calculated, but seems like it should be using the field /grid cell average surface roughness length?
I dont know, but as far as I understand for many regions 100 m should be above "blending height", i.e. the wind conditions should be more or less independent of the underyling surface at that height.
- "ECMWF creates these fields using a 'blending height' (40m since 2013)," (1)
- At blending height, "concentrations and meteorological parameters are not influenced by surface properties to a large extent”. (2) In this book, they use 50 m as blending height.
- https://glossary.ametsoc.org/wiki/Blending_height
Let me know if this does not make sense 
(1) 9.3 Surface Wind
(2) Erisman, J. W.; Draaijers, G. P. J. (Hg.) (1995): Atmospheric deposition in relation to acidification and eutrophication. Amsterdam, New York: Elsevier Science. Online verfügbar unter http://worldcatlibraries.org/wcpa/oclc/162130777.
Thanks Andreas, that was very helpful.
I'm interested in how to extrapolate the ERA5 wind speed at 100 m to hub heights of wind turbines in the the 50-200 meter range. The log law of the first part of eq. 3.92 in the IFS Cy41r2. PART IV: PHYSICAL PROCESSES documentation is often used for such extrapolation:
But I'm unsure about what z0 to use when using ERA5 100 meters wind as reference. Is the ERA5 forecast roughness length (fsr) of the grid average representative well above the blending height or should the z0 just be something small like 0.03 at those height?
Hi lukas,
I‘m also interested in both interpolating and extrapolating the ERA5 wind speed at 10m and 100m to the height that I am concerned.
I tried to calculate the wind speed at 50,80 meter, using logarithmic profile with the forecast surface roughness (fsr) and wind speed at 10m (u10, v10) from ERA5 houly reanalysis dataset. The result shows that the annual average of wind speed at 50m oversea is almost the same as that at 100m(ERA5 100m wind speed), while the annual average of wind speed at 80m oversea is larger than that at 100m, which can be considered to be wrong.
As you mentioned above, ERA5 10 meter wind is calculated with z0=0.03. So maybe my way to get 50 meter and 80 meter using ERA5-10m wind speed and forecast surface roughness is wrong.
Hi Lukas,
if I understand the documentation correctly, it only says that the 10 m wind speed is "post-processed" to match the usual measurements over grassland (i.e. wind speed is converted to a hypothetical z0_WMO of 0.03m). I do not see a similar statement for the 100 m windspeeds, so I would guess that the 100 m wind speeds reflect the actual land-use average z0 of the respective grid-cell. But note that this is just a guess.
In section 3.2.4 "Roughness lengths" in the document you mentioned it says "The roughness lengths over land are assumed to be fixed and related to the land surface
cover." The corresponding values are listed in table 8.3. They range between 0 and 2 m. In the formula you posted, if you replace z10 and zblend with large numbers (e.g. 100 m and 40 m), it might not mattern which z0 (0.03 m or 2 m) you use. This would reflect that the underlying land use (z0) does not matter so much at these large heights. I am not sure about this.
A while ago I came across this paper, they might be doing what you also intend to do without needing a z0: https://www.mdpi.com/1996-1073/14/14/4169
Thanks again Andres. Yes, that power law from the paper you mention probably makes more sense for higher height where the surface roughness shouldn't matter. Saw this post as well, ERA5: How are the 100m winds calculated?, that tells that the wind at 100m is calculated using interpolation on the log scale, which I think mathematically is the same as using the power law used in the paper you linked (at least in the case linear interpolation).
This site says that the log law is appriate for the lowest 100m katabatic power (ucsc.edu).
Hi Lukas, thanks for the update!
Hi all,
I am interested in this discussion, as I am looking into how the 10m and 100m wind field from ERA5 are calculated.
Do you have any further information to share, beyond what you have give above, about how the 100m wind field is calculated? What laws/profiles have been assumed? etc.
Any reference or advice would be welcomed.
Cheers,
Sara
Hi Sara Jackson, Folks,
two datasets of windspeeds at several heights are
KNMI https://dataplatform.knmi.nl/ https://en.wikipedia.org/wiki/Royal_Netherlands_Meteorological_Institute
at 10 20 40 .. 200 .. 600m on a ~ 2 x 2 km grid
and GWA, https://globalwindatlas.info) at 50 100 150m on a 0.0025° grid.
The two models of height -> windspeed may of course differ:
powerlaw aka Hellmann: 6.45 * (h / 100) ^ 0.25
log-ratio: e.g. 5.5 * ln( h / z0 ) / ln( 30 / z0 )
Fitting windspeed ~ (height / 100) ^p to the Netherlands data at the sites of half a dozen windfarms
seems to fit the Netherlands data pretty well, with powers
[0.086 0.088 0.091 0.1 0.16 0.16 0.17 0.18 0.19 0.19 0.23 0.24]
I haven't tried fitting z0 -- cf. Kruyt.
(In Germany, assessors used log-ratio wih z0=0.1 until 2017, powerlaw 0.25 after that,
over the whole country ! see https://de.wikipedia.org/wiki/Referenzertrag.)
Does anyone know of more data of windspeeds at > 2 heights and different kinds of terrain --
flat, forest etc. preferably in Europe, onshore ?
Notes:
1) why at the sites of windfarms ? easy importance sampling -- that's where the wind and the money is
2) most NL windfarms are near the coast, so untypical for e.g. south Germany
3) don't fit powerlaw in loglog space, fit directly -- scipy least_squares worked well.
Kruyt et al., A Downscaling Intercomparison Study: Models of Different Complexity
https://infoscience.epfl.ch/record/292722/files/feart_2022 says
"We have chosen not to use a log law to correct for height
due to strong uncertainties associated with the choice of the roughness length"