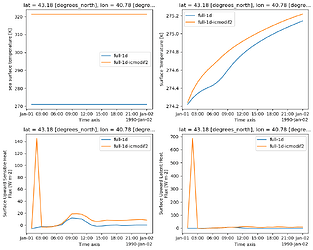
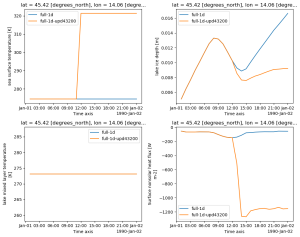
Admittedly SST over land sounds pretty weird, so why bother? The initial conditions for OpenIFS contain SSTK in the ICMGG*INIT file with reasonable values over the ocean. Over land the values are close to 273 (K) bot not exactly the same everywhere. For some EC-Earth development I changed the value of SST over land, and found it had an impact on the result. I was able to crate similar differences when changing the SST in the initial conditions. Here are timesries from a gridpoint at the Black Sea coast in Georgia:
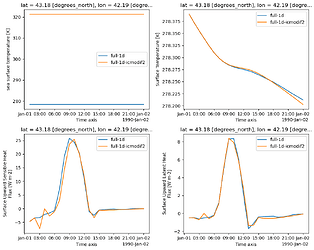
The blue line is the control, and for the orange line the SST in all land points (i.e. where CL LSM>0.5) has been replaced by 321.35. The plots show SST, surface temperature, sensible and latent heat fluxes in this point. There is a dramatic heat flux during the 2nd timestep. Interestingly enough, the gridpoint next to this point doesn't show any response to an SST change:
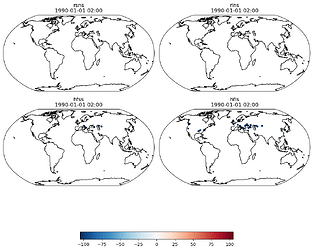
Here is a map indicating where heat fluxes during the 2nd timestep get unusually high:
It's not everywhere, but there are a few gridpoints where heat fluxflux seem off. It's not just along coastlines, it can also happen in the interior of land. It seems to be unrelated to lakes.
The thing that puzzles me is that the value of SST over land shouldn't play any role. There is no value for missing/undefined in GRIB, therefore there must be some value for the SST even over land in the initial conditions which is usually never updated during a simulation and constant over time. The IFS documentation Part IV Section 8.2.1 clearly states: "A mixture of land and water (ocean/inland water) tiles is not allowed, i.e. a grid box is either 100% land or 100% sea." Thus, any value of SST shouldn't be used anywhere in the surface scheme where CL LSM>0.5. However, my tests that change SST over land points tell something else.
Could there be a bug somewhere in the surface scheme that uses SST for some computations even in gridpoints over land?
Sorry, there is a terrible mistake in teh description above, land points are points with LSM>.5 (CL is the lake fraction). The plots are correct, show the results for the case with SST=321.35 where LSM>.5 (= land point)
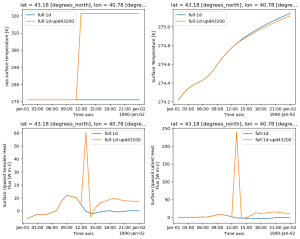
One may argue that the initial conditions are somewhat special in that SST may have been used somehow when setting soil temperature, or skin temperature, and replacing only SST in the initial conditions could thus destroy the balance in the initial state. To test the hypothesis I have set up a nwe experiment in which SST is untouched in the initial conditions, but 12 hours into the run it is set to 321.35 K in all gridpoints with LSM>.5. I get the same result as before, the heat fluxes become unrealistic right after the update in some slected points but not others:
My colleague Chema made similar tests with plain OpenIFS 43 (my tests were with OpenIFS 43 in EC-Earth4) and found siilar differences when SST over land points is updated. He then tested updating SST only over land points that have no lake ice, and this test turned out to have no impact. The conclusion is that somehow a change in SST over land interferes with lake ice!
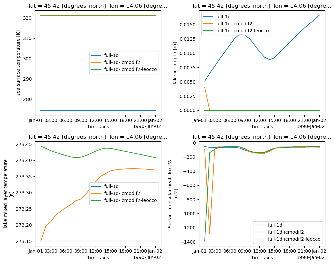
Here is another example from a gridpoint where the lake ice doesn't disappear yet there is a strong impact after SST changes in this point at 12 Z. The blue line is the control experiment in which SST doesn't change. Note the strong change in non-solar heat flux (=str+slhf+sshf) after 12 Z (lower left) in the experiment with changing SST. The lake ice is very thin, less than 1 mm.
Are such strong heat fluxes realistic? And why do we get this jump in heat flux when SST over land is updated?
Hi Klaus, thank you for raising this here on the forum. I've passed this on to the relevant team and I hope that you will soon get a response about this issue.
Best, Marcus
Hello Klaus Wyser,
Thanks for your plots. As your investigation suggest, this should be related to the fact that tile 1 (ocean) is used in case a lake is partially frozen (ice depth < 10cm).
This is done to account for a mix of non-frozen and frozen lakes within a grid cell, which can have a large impact on the surface fluxes.
I think the problem here is that SST can be wired into the surface energy balance calculation if the cold skin or warm skin parametrizations are turned off (see namelist flags: LEOCWA , LEOCCO),So eventually changing the results. Can you have a look at it?
Cheers,
Gabriele
Thanks a lot for your comment, appreciate.
But why is tile 1 used over land gridpoints? The manual clearly says that any gridcell is ether 100% ocean (tiles 1 and 2) or 100% land (tiles 3-9), no mixtures. It then doesn't make sense that SST is used for the temperature of a partly frozen lake, or am I missing anything?
And another comment: the lake mixed layer temperature (lower left in my last figure) doesn't show any change when SST changes, it's always 273.15 deg in this specific point. So why would heat fluxes become different then?
Hi Klaus,
Could you confirm that LEOCWA , LEOCCO are set to false in your namelist? Just to be sure that indeed this is the pathway taken in the code.
The land-sea mask of the model is binary, so a grid point is either 100% ocean or 100% land. Once it is decided a grid point is 100% land, then tile 1 can be used in case of partially frozen lakes. The documentation should be updated to better describe this behaviour. On one hand, this allows to account for partially frozen lakes without having to include two specific "ice-lake" and "water-lake" tiles, if it makes sense. Also, it allows to take into account the large difference in heat fluxes and their impact on the lake prognostic variables evolution; as you show in your plot with the different evolution of lake ice depth (though for the wrong reason, as driven by SST).
I agree that SST should not be used in these cases, and I think it is an undesired behaviour if LEOCWA and LEOCCO are turned off. In case Cold/Warm skin parameterisations are turned on the model would use these parameterisations for the evolution of the skin temperature of tile 1, if I am not mistaken (we can double-check the details if needed).
Lake mixed layer temperature is bounded to 273.15 and an increase in heat flux would trigger ice melting (ice depth decreasing), so I think the behaviour you see in your plots is consistent.
Thanks a lot Gabriele for the detailed reply. I checked my experiments and they have ``LEOCWA=F`` and ``LEOCCO=T``. I found two slightly different experiment (SST over land grid points has been modified in initial conditions), comparing ``LEOCCO=T`` (orange) and ``LEOCCO=F`` (green). The plot shows the timeseries of SST, ice depth, lake mixed layer temp, and total non-solar heat flux.
The outcome is different in the first timestep, but common for both experiments is that there is a timestep when the ice disaapears with huge (and unrealistic) negative non-solar heat flux. So yes, the setting of LEOCCO plays a role, but it's not the cause of the more general problem that we get this huge flux.
[...] a grid point is either 100% ocean or 100% land. Once it is decided a grid point is 100% land, then tile 1 can be used in case of partially frozen lakes.
That's strange, if tile 1 is used for land gridpoints then I wouldn't call it 100% land any longer because it uses SST in that point (from the initial conditions).
Wouldn't it be better to use the lake mixed layer temperature for the open water temperature instead when computing skin temperature and heat fluxes? The only problem with that approach could be coastal points with ``CL>.5`` where we could get a temperature jump between the coastal point and adjacent ocean point. But on the other hand, this could also happen if SST from the initial conditions is used that doesn't match the actual SST.
Finally I found some time to look into this again. Thanks to Gabriele's explanations I think I now understand the intention to use tile(1) even with lakes. Tile(1) is used for the open water fraction when lakes are covered by fractional lake ice and the reason is likely that FLake itself cannot account for fractional ice cover. In gridpoints with lake cover between 0 and 1, tile(9) is scaled with the ice fraction and the rest - up to PCL - is then filled by tile(1). If all lake ice has melted, the lake fraction is again set to PCL.
The intention with fractional lake ice cover may be good, but there are 2 problems with using tile(1) for lakes:
- Physical parameters may be different for ocean and for lakes, for example the albedo
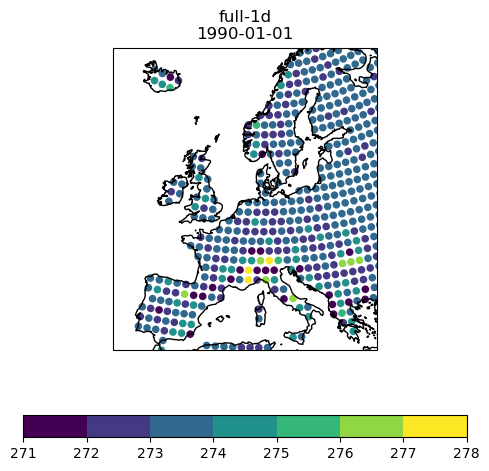
- The temperature in tile(1) over land is rather arbitrary, unclear where it comes from. Here is a plot of SST over land for Jan 1, 1990 (from the initial conditions):
The source of these SST values is unclear. These are the temperatures that are used for the open water fraction of lakes if the lake ice fraction is between 0 and 1. It is rather obvious that values of 5 deg C are not very meaningful.
I wonder if we wouldn't be better off by using only FLake for lakes, accepting that lakes are either fully open or fully covered by lake ice. The lake ice thickness varies which ensures that the effects of lake ice on heat fluxes and albedo are shifting smoothly from open water to ice. Isn't that good enough?
Hi Klaus,
thanks for your message.
I agree that there are limitations in using this approach and parameter choices might be revisited in the future, but for global NWP application it is still a better solution that letting the entire lake fraction freezing for lake ice depth > 0 , which is not really realistic (I am not a lake expert but lake freezing is not a spatially homogenous process).
The SST values over land, in your configuration, would come from the initial conditions. In more recent cycles we enforce the SST over land to be equal to the lake mixed layer temperature, which is computed over every grid point even if the lake fraction = 0. This allows to have a more "realistic" temperature in the SST field.
Hope this helps.
Cheers,
Gabriele
Thanks Gabriele.
Would you know why SST over land in the IC's vary from one gridpoint to another? See an example above.
Yes, we could use one of the lake temperatures to fill SST over land. However, I'd rather not abuse the SST field for that because I would like to compute ocean fluxes even over land points. This may sound strange but is required in the coupled model if the land-sea mask of the atmopshere and ocean models don't match.